Euro-SiBRAM’2002 Prague, June 24 to 26, 2002, Czech Republic
Session 9
On the use of reliability assessment methods for structural design
Göran A. Alpsten, Former Adjunct Professor at KTH, Stockholm
Stålbyggnadskontroll AB, Bergshamra Allé 139, SE-170 77 Solna, Sweden
goran.alpsten@stbk.se
This contribution will discuss the use of reliability assessment methods, such as the SBRA simulation technique developed by Pavel Marek and coworkers, see for instance [1], [2], for practical design of load-carrying structures. For practical reasons this discussion will focus on steel structures, with a background of Swedish conditions. Steel is used extensively in Sweden in structures, such as multi-story buildings, industrial buildings, chimneys and bridges. For instance, some 80 percent of multi-story office buildings in the Stockholm region built in recent years have a steel frame.
The use of simulation techniques is possible through the advances in computer technology. All major structures today are designed using computers, in one way or another. While today's computers present a formidable tool for the design of structures there is also a potential danger that the experience and engineering judgment of a skilled designer may be replaced by an uncritical adoption of nicely presented results from a computer program, the assumptions and limitations of which the designer is not completely aware of. The writer has seen too many examples of this in practice, in particular in relation to the use of computer software for design and presentation of steel structures on drawings and specifications.
The partial factors method has been used in Sweden for about 20 years, and I think designers on the whole are quite happy with that method. It might be argued whether this is a "semi-probabilistic" method, but I think its development has contributed to a better understanding of uncertainties in the design of structures.
Different structures and various components in a structure should be designed on the basis of an accepted level of safety for the particular structure or component. The current Swedish regulations for load-carrying structures BKR 99 [2] has adopted safety classes as a procedure to account for this. For the three safety classes defined in BKR 99, and for accidental action and progressive collapse, reliablility index values b according to an ISO standard [3] are given in BKR 99 for probabilistic design procedures, as shown in Table 1. Although conditions thus exist in the regulations for applying a probabilistic design approach we have not seen many, if any, applications of such methods in the design of actual structures. For design using the partial factors method various partial factors are given to account for the consequences of a failure of a particular member, see Table 1. This is in addition to the partial factors for loads, normally 1.3 for one live load at characteristic level and 1.0 for dead load and other live loads at reduced ("ordinary") level.
Table 1 Reliability index values b and partial factor gn to account for consequences of a failure, as given in Swedish regulations BKR 99 [2]
Safety class etc. b Partial factor gn
Safety class 1 3.7 1.0
(small risk for serious personal injury)
Safety class 2 4.3 1.1
(some risk for serious personal injury)
Safety class 3 4.8 1.2
(high risk for serious personal injury)
Accidental cases 3.1 1.0
Conditions for progressive collapse 2.3 1.0
Safety of structures, gross errors
Experience shows that the reliability as determined from the variation of relevant variables affecting load effects and capacity of structures does not present the full picture. In fact, from the over 200 cases with failures or "near-failures" in which the writer has engaged as an investigator it is evident that most of these cases were not the cause of foreseen variation of variables but a result of gross errors. These include grave mistakes by the designer, snow loads being two or three times greater than specified from 50-year data, strength of steel reduced to almost zero due to center-line segregations of modern steel produced by continuous casting, welds which are non-existent or just a tack weld, interchanged diagonals in a steel truss etc, bolts in a connection which have corroded to just a small fraction of the initial cross section. A few examples of such experience were presented at the Colloquium.
How to incorporate the risk for gross errors in reliability assessment using Monte Carlo simulation? It may be easily said that gross errors should be eliminated by checking of design calculations and inspection of execution of structures. However, even a meticulous scrutiny will not completely eliminate the risk of gross errors.
Incidentally, there is a tendency in modern quality assurance procedures to focus on formal QA schemes, more or less replacing down-to-earth inspection of the actual physical structure. I believe this might prove detrimental to the reliability and safety of structures.
The effect of gross errors may in some cases be included in the distribution of the appropriate variable, or using a mathematical framework as discussed briefly in [2]. In the present situation the effect of gross errors is a big black box to the designer, when applying the partial factors method and simulation techniques as well. For a truly probabilistic design we have to address this matter of gross errors in a more rational way.
Statistical distributions of variables entering the design of structures
For a probabilistic assessment in structural design of real structures it is important to have a fair knowledge about the variation of relevant variables affecting the strength and serviceability criteria of the structure. The results of even a very advanced simulation using finite-element software are not more reliable than the input data supplied by the user.
A lot of data for the variables entering the design of load-carrying structures is compiled in the documents on the SBRA technique, such as [1,2]. However, for a rational and accurate reliability assessment more data would be needed. I think the data furnished in various textbooks on the use of simulations techniques are fine for demonstration and educational purposes, but they may not be appropriate for accurate design of real structures. It is believed that much data exist in many places which may not have been published. A compilation of such data would be of great practical interest.
The writer would like to draw attention to some data for European structural steel grades and hot-rolled members which may not be easily found in the readily available literature.
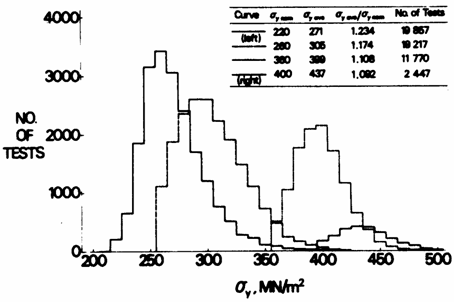
A compilation of strength data from some 53 000 tension tests of structural steel at various steel mills was presented in [5]. Some data are reproduced here, see Figure 1 and following. The yield strength of the tests is the yield strength level on the yield plateau, which is more adequate for most design purposes than the upper yield point often reported in conventional tension testing.

Figure 1 Yield strength of some 53 000 tension tests of structural steel of different grades, corresponding to the present S235x up to S420x European grades [5].
As can be seen in the diagram of Figure 1, and is evident from Figure 2 for one of the steel grades in Figure 1, the variation of yield strength is skewed to the right, and is not well represented by a normal distribution. On the other hand, the variation may be well represented by a shifted log-normal distribution, Figures 2c and d, or by an extreme-value distribution type I, Figures 2e and f. The ordinate scale in the CDF diagrams in Figure 2 has been transformed in such a way that the parametric distribution in question will plot as a straight line. One reason for the skewness of the distribution is the fact that the process of manufacturing structural steels in a modern steel mill is kept under strict control by adding alloying elements such as manganese etc. as required. It will normally be more economical for the steel producer to add a little extra alloying elements than to risk having a complete charge not fulfilling criteria.
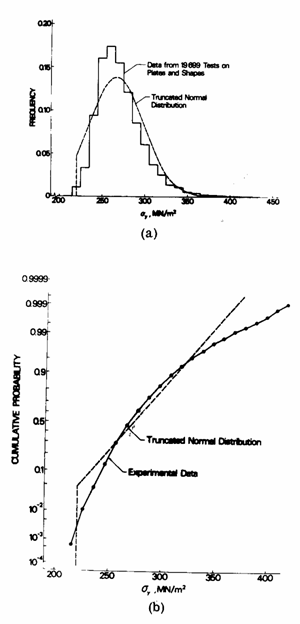
Figure 2a+b Example of probability density and cumulative distribution functions for yield strength of a steel grade SIS 131X equivalent to S235JR in EN 10 025 [5]. Ordinate scale transformed in such a way that a normal distribution will plot as a straight line.
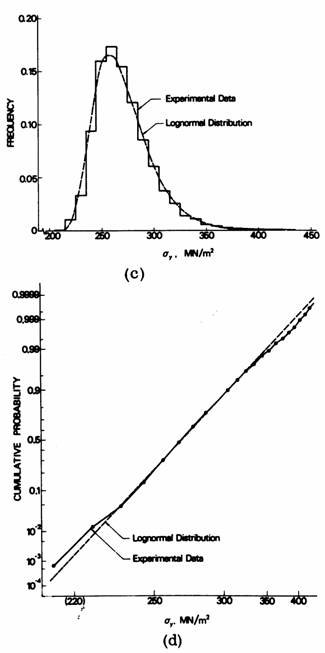
Figure 2c+d Example of probability density and cumulative distribution functions for yield strength of a steel grade SIS 131X equivalent to S235JR in EN 10 025 [5]. Scales transformed in such a way that a normal distribution will plot as a straight line.
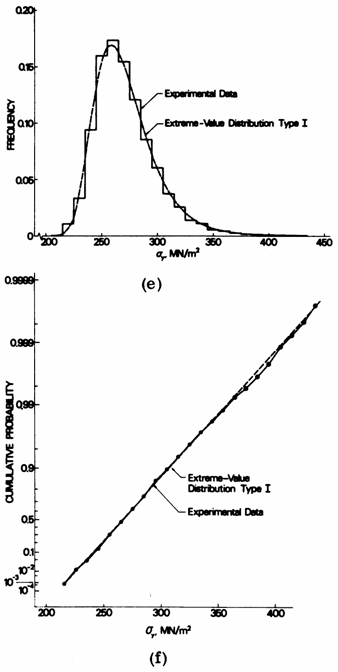
Figure 2e+f Example of probability density and cumulative distribution functions for yield strength of a steel grade SIS 131X equivalent to S235JR in EN 10 025 [5]. Ordinate scale transformed in such a way that an extreme-value distribution type I will plot as a straight line.
Below will be reviewed the variation of the moment capacity related to the cross section of rolled steel members. Therefore the variation of yield strength of hot-rolled structural H- and I-shapes has been extracted from the data in Figures 1 and 2, as shown in Figure 3. It appears from the diagram that the flange thickness of the member is a statistically significant variable for the yield strength of the member.
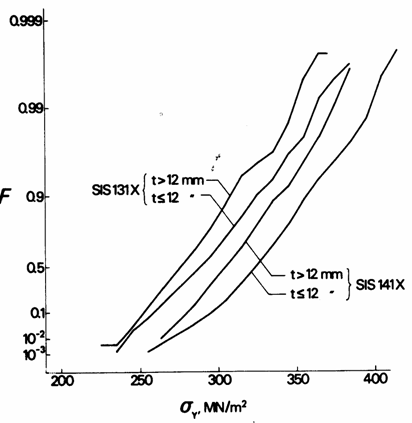
Figure 3 Data for yield strength of tension tests of specimens taken from structural H- and I-shapes of two common structural steel grades equivalent to S235JR (SIS 131X) and S275JR (SIS 141X) in EN 10 025 [5].
The capacity of a structural member under various types of loading is dependent upon its cross-sectional properties. Figure 4 shows the variation of cross-sectional dimensions as measured on 4 816 H-shapes rolled at several European steel mills [5]. It is clear that the relative variation in height and flange width is small compared to the variation in thickness of the flange and web. There is a tendency of the flanges being thinner and the web being thicker than the nominal. The reason for this is probably an economical optimization of the adjustment and replacement of the rolls due to wear, within the prescribed rolling tolerances. Since rolling tolerances are given both for individual dimensions and cross-sectional area of the member under-thickness of the flanges may to some extent be matched with over-thickness of the web, creating a member cross section with a greater web-to-flange ratio.
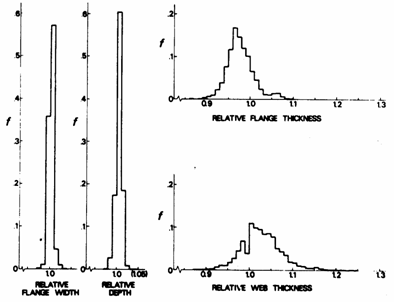
Figure 4 Variation of cross-sectional dimensions of 4 816 H-shapes of structural steel rolled at various European steel mills [5].
a)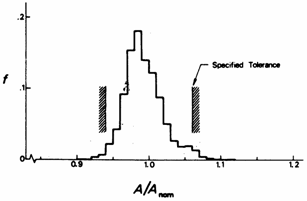 b)
b)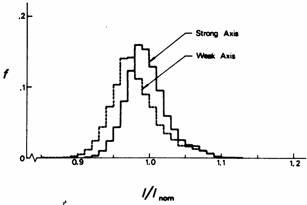 c)
c)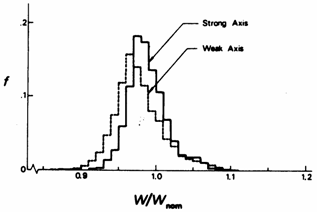 d)
d)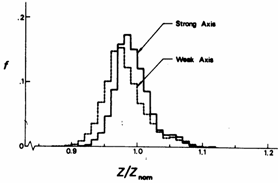
Figure 5 Variation of cross-sectional properties of hot-rolled H-shapes [5] determined from the cross-sectional dimensions of individual members given in Figure 4.
For simple statistical relationships, such as Z = XY or Z = X+Y, where X and Y are independent stochastic variables defined by non-parametric histograms, straight-forward numerical integration of the distribution for Z can be easily made requiring just a small fraction of the number of numerical operations for a Monte Carlo simulation. The moment capacity of a beam cross section Mel = fy W or Mpl = fy Z may easily be obtained this way, see Figure 6 below. Using such simple numerical techniques in connection with Monte Carlo simulations for reliability assessment may reduce the number of simulations required, which may be of practical interest for the design of systems or complicated components requiring large-scale finite element calculations.
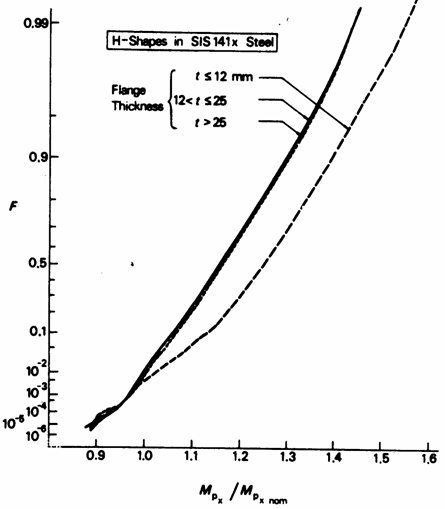
Figure 6 Variation of plastic moment Mp about the strong axis of rolled H-shapes deduced from the variation of yield strength of Figure 3 and cross-sectional properties of Figure 5 using a numerical integration, assuming these two variables to be statistically independent within three intervals of the flange thickness [5].
While the data reviewed so far was published about 30 years ago, some recent information from an experimental long-term study of a 90 m high steel chimney with continuous measurements of wind data and structural response will be briefly referred here [6]. The chimney has a friction-type damper at the top, which did not work properly in the first few months, causing heavy vortex shedding and fatigue cracks after five months of service. The damper was found to be defective because transport fixings had not been released properly after the erection. This was corrected and the fatigue cracks were repaired, but in order for the owner of the plant to accept the chimney a monitoring system was installed, with recording of wind velocity and direction, and load effects in the chimney.
Only an example of the distribution of the 10s mean wind velocity, Figure 7, and the load action (top displacement of the chimney), Figure 8, is reproduced here. The interested reader is referred to the original report [6], which contains extensive data for a four-year period from 1997 through 2000, including ants-hill diagrams for wind speed, wind rosettes, load action and load action spectra for determining fatigue behavior.
As may be observed from the diagram in Figure 7 the wind velocity data is well represented by a Weibull distribution. This applies for wind-velocity data for 1 minute and 10 minutes as well. The reason for the deviation in the low range is that data was measured but not recorded for winds causing top deflections less than 100 mm. Smaller variations would cause negligible effects with respect to fatigue of the steel structures of the chimney.
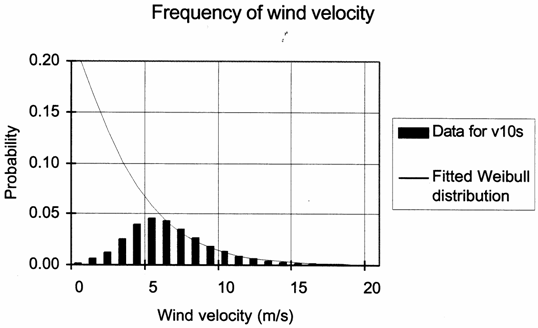
Figure 7 Data on 10-s mean wind velocity measured over a four-year period 1997 through 2000 at the site of a 90 m steel chimney at Vaxjo, Sweden [6].
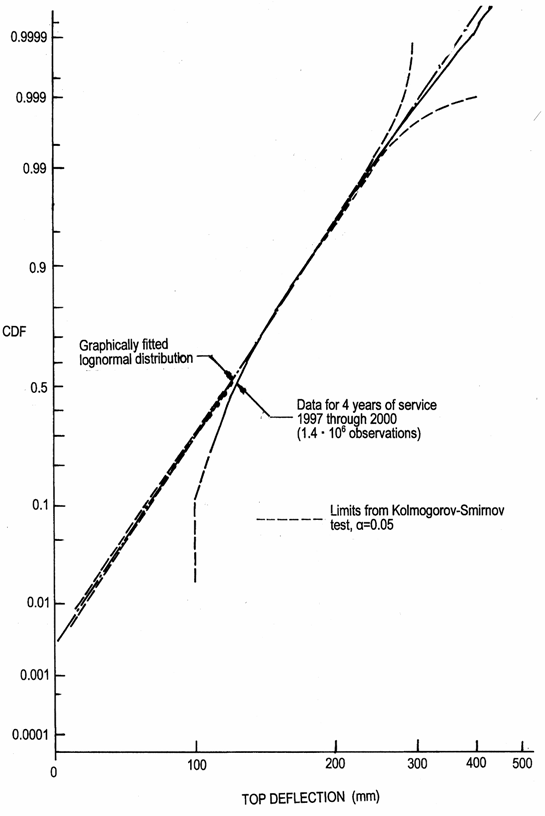
Figure 8 Variation of top deflection of a 90 m steel chimney at Vaxjo, Sweden measured continuously over a four-year period 1997 through 2000 [6].
In many examples discussed in the literature on probabilistic design distribution of variables has been assumed to follow a normal distribution, even when non-parametric representation has been used. From the scattered examples shown here and other experience it appears that a shifted log-normal distribution may in many cases give good fit to measured or observed data. For a non-parametric representation, such as used in bounded histograms in the SBRA technique, parameters of parametric distributions may be of limited use. However, when bounded histograms to be used in a simulation have to determined from a limited amount of actual data, knowledge about a probable underlying distribution should be useful.
Structural models
Many examples of Monte Carlo simulation presented in the literature on SBRA use simplistic structural models for the structural behavior. Although this may be useful in presenting the technique and for educational purposes, practical probability-based designs should preferably be based on more accurate models, such as finite element models.
Why use simple structural models of the slide-rule era, such as simplified interaction formulae, when a computer is at hand? Numerical models for simulation of, for instance, the buckling behavior of a steel column with actual distribution of residual stresses, variation of yield strength over the cross section, out-of-straightness of the column (which may not always be a perfect sine curve), end eccentricities etc. are available but appear presently not to be extensively used in the reliability assessment of actual structures.
Conclusions
The items discussed in this contribution may be summarized as below:
Adopt ways to consider the risk of gross errors in the reliability assessment procedures.
Compile data and present in a codified form readily adopted by practicing engineers.
Demonstrate probabilistic design with the use of modern computerized methods such as finite element methods for modelling the structure, not only simplified representations such as interaction formulae.
For a fully probabilistic design, simulation considering the true structural behavior may be used in practical design.
It is proposed that methods for assessment of structural reliability such as the Monte Carlo and other simulation techniques should not be presented as a replacement to "conventional" design methods but a rational alternative to current techniques employed by structural engineers. I think we should be content with that probabilistic methods of design be used mostly for special structures, where great savings are offered by a more rational design procedure.
References
[1] Pavel Marek, Jacques Brozzetti & Milan Gustar (editors): Probabilistic assessment of structures using Monte Carlo simulation. Background, exercises and software, ITAM, Academy of Sciences of the Czech Republic, Praha, 2001.
[2] Pavel Marek, Milan Gustar & Thalia Anagnos: Simulation-based reliability assessment for structural engineers, CRC Press, 1996.
[3] Regulations for load-carrying structures, BKR 99, Swedish National Board of Housing, Building and Planning, November 1998.
[4] General principles on the reliability for structures, ISO 2394, 1998.
[5] Göran Alpsten: Variations in mechanical and cross-sectional properties of steel, State of Art Report, Proceedings of the International Conference on the Planning and Design of Tall Buildings, ASCE-IABSE, Lehigh University, August 1972.
[6] Pär Tranvik & Göran Alpsten: Dynamic behaviour under wind loading of a 90 m steel chimney, Alstom Power Sweden AB, Växjö and Stålbyggnadskontroll AB, Solna, Sweden, March 2002.
[7] Göran Alpsten & Pavel Marek: Structural design of load-carrying structures - From safety techniques of the slide rule era to reliability assessment techniques making full use of today's computers (in Swedish), Paper in preparation.